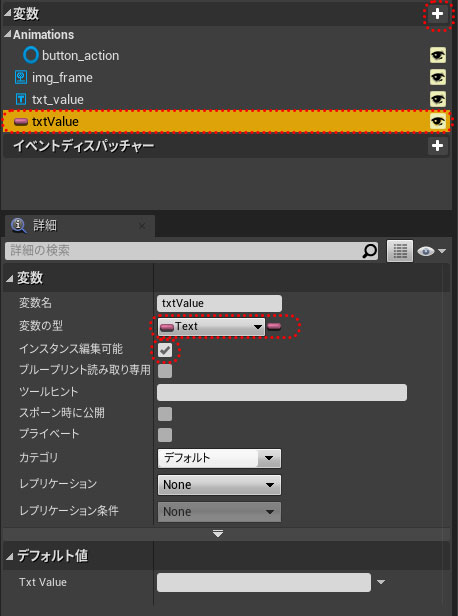
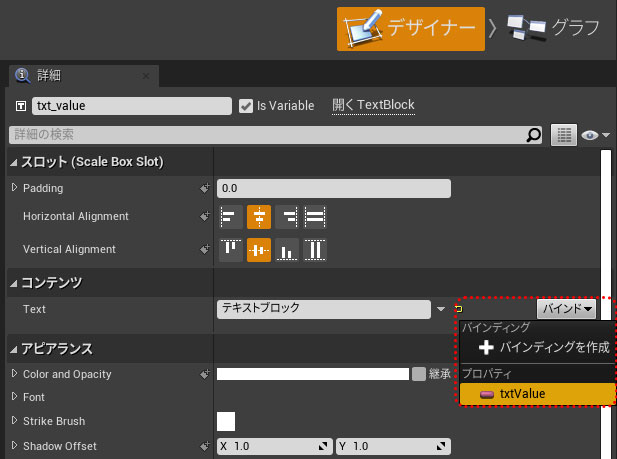
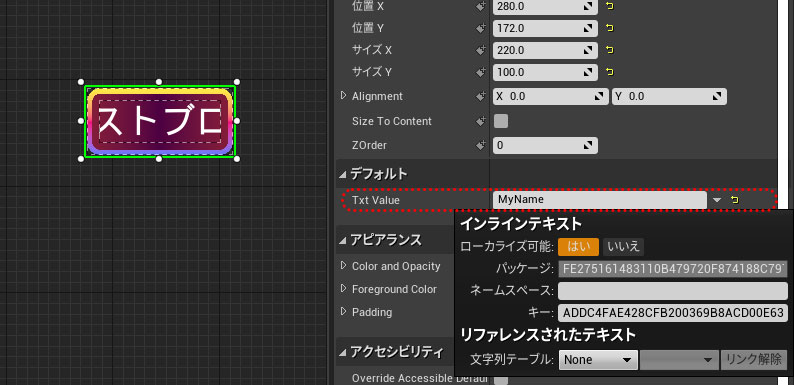
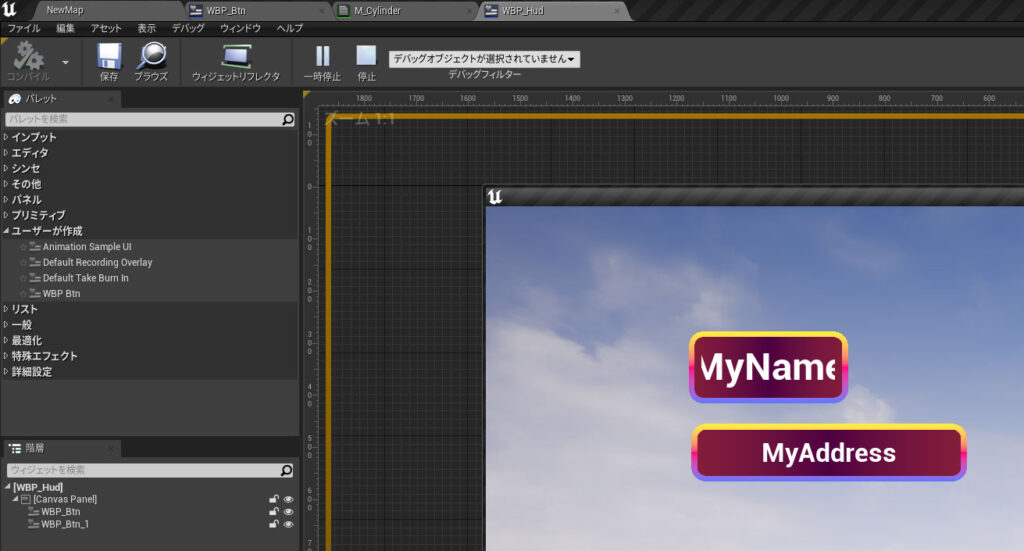
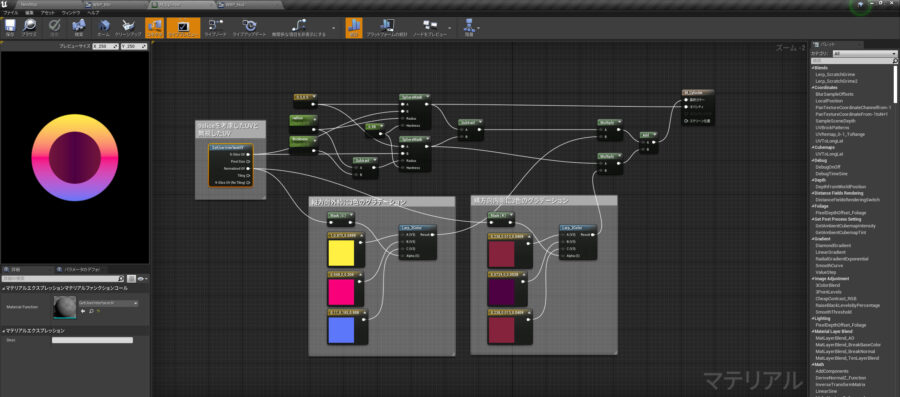
UMGの持つトランスフォーム機能は「移動」「回転」「拡大」「シアー」の4つがあり、幾何学的にはアフィン変換と呼ばれる座標変換処理にあたるもので実現されています。
UI実装者はこの機能を使いレイアウトやインタラクション実装を行っていますが、この仕組みだけでは物足らないと感じる場合があります。特に疑似的な立体表現としての台形への変形を行いたい時でしょう。(Photoshopでいうところの「自由変形」のように処理したい)
例えばUBISOFTの『DIVISION2』やプラチナゲームスの『アストラルチェイン』などではプレイヤーのステータス画面の実在感を高めるため、3Dのプレイヤーモデルとの位置関係を空間的にし、若干の傾きを持った板のように表現しています。ただこれらは実装上はレベル内に配置した一枚の板ポリゴンにUIレイヤーを張り付けた、いわゆる3DUIと呼ばれるものではないかと思われます。
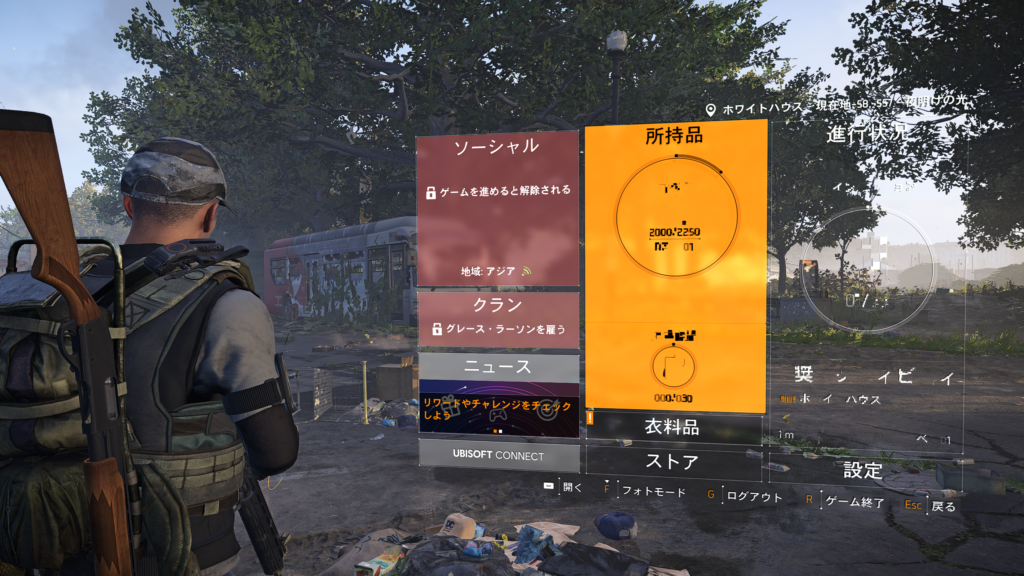 『DIVISION2』台形に変換されたプレイヤーメニュー
『DIVISION2』台形に変換されたプレイヤーメニュー
UEにもアクターにウィジェットBPを張り付けて3DUIとして扱う機能は存在しますが、3DUIは一般的に取り扱いが難しく、特にビューポートにレイアウトを固定したい要素については結局カメラとの位置関係や挙動を構築するのにコストがかかってしまうため、細かいちょっとした要素に使うには向いていません。
(蛇足ですが、サイバーパンク2077やDESTINY2ではHUDにレンズ的湾曲表現を取り入れており、プレイヤー目前にあると思わせるモニター感を生んでいて好きな表現です。ただしこれはHUD全体のポストプロセス処理が必要になるので一般的に重いと言えます)
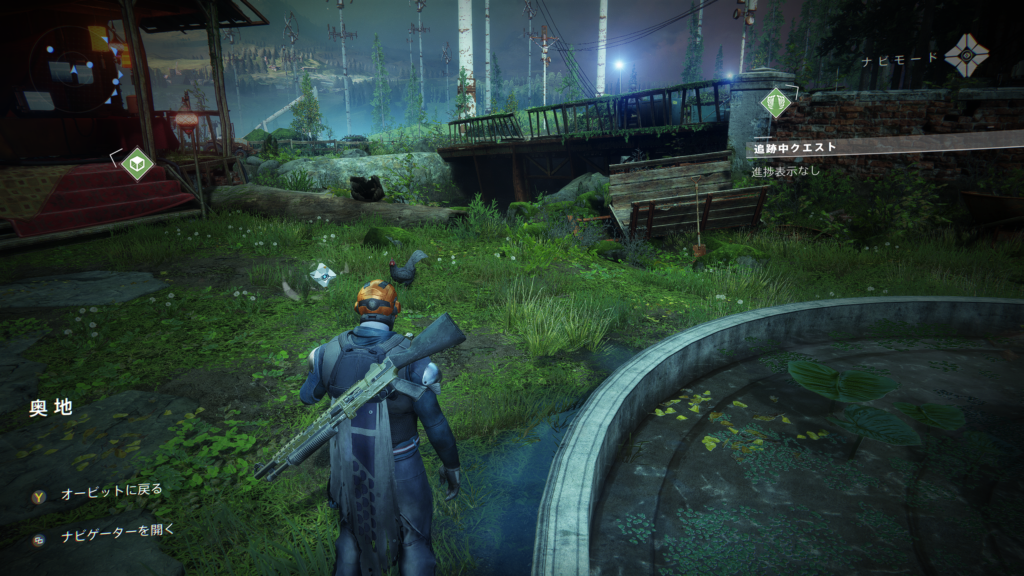 『DESTINY2』レンズ効果ポストプロセスを含んだHUD
『DESTINY2』レンズ効果ポストプロセスを含んだHUD
つまり固定的なレイアウトが必要で、さらに要素の前後関係を制御する必要がある場合、できるだけ2DUIで実装する必要が出てきます。
アフィン変換と射影変換(ホモグラフィー)
そこでウィジェット用のマテリアル内でUVを変形させてしまうという手法を考えるわけですが、ここで出てくるのが射影変換(ホモグラフィー)という変換方法です。
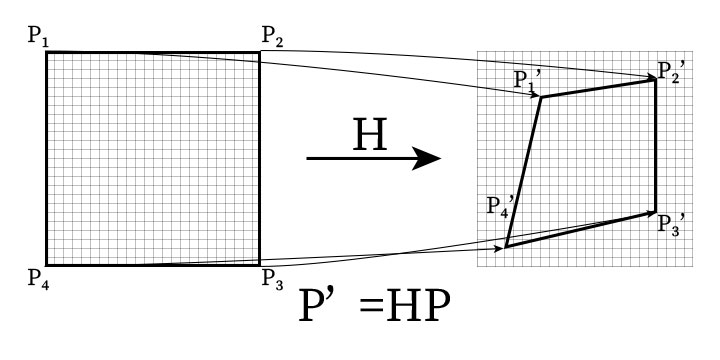 射影変換のイメージ
射影変換のイメージ
これは幾何学的にも前述したアフィン変換を包括する関係にありますので将来的にはUMGグラフ画面での基本機能としても実装できるのでは…とエピックさんにお願いしたいところですが、現状ではないものねだりなので何とか自前で対応します。
今回の手法では矩形のテクスチャを(0,0)(1,0)(1,1)(0,1)の座標系でとらえ、(x0,y0)(x1,y1)(x2,y2)(x3,y3)の4点を頂点とする座標を結ぶ自由矩形に変形する、という機能に限定します。UEにはRetainerBoxという特殊なUMG部品があり、配下部品をレンダリングしたものを一枚のテクスチャとしてマテリアル内に展開できるという便利な機能があるため、これを組み合わせることを考えると相性が良いやり方のように思います。
射影変換の考え方などは各種ブログエントリなどにありますのでここでは書かず、あくまでUEのマテリアル実装について絞っていきます。いろいろググっていくとUnityでホモグラフィー変換を実装している方がいらっしゃったので、これに乗っかってUEのマテリアルノードに移植してしまいたいと思います。
UEのマテリアルノードへの移植
こちらのエントリにAPIのソースコードへのリンクが記載されています。
入力座標が (0.0, 0.0)、(1.0, 0.0)、(1.0, 1.0)、(0.0, 1.0) と出来るため 8 次元連立一次方程式は割りと綺麗に解くことが出来ます
Unity で画面出力を変形するイメージエフェクトを作ってみた
(僕は投げ出しました…凹みさんありがとうございます!)
このうち、GetInverseHomographyPositionが対応するものになるのでUEのマテリアル関数として移植します。
ソースコードに対応するように下記のノードに分けることにしました。
GetInverseHomographyPosition
CalcInverseMatrix
CalcHomographyMatrix
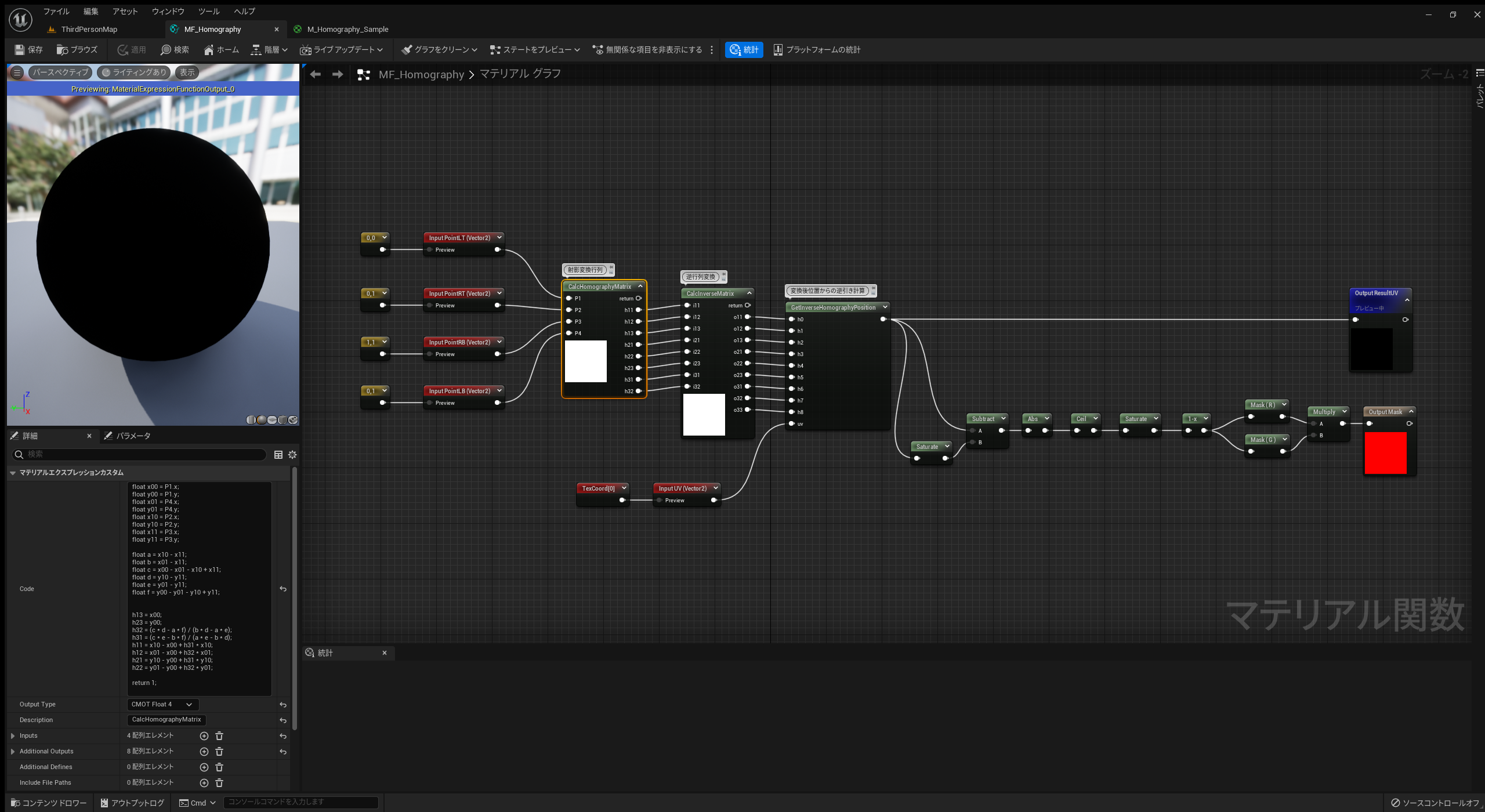 ホモグラフィー変換用マテリアル関数 MF_Homography
ホモグラフィー変換用マテリアル関数 MF_Homography
それぞれカスタムノードを使うことでそれぞれの導出式を組み込んでいきます。カスタムノードのinput/outputを複数持てるようになったのはありがたいですね。
[CustomNode]CalcHomographyMatrix(射影変換行列)
4頂点の座標をinputとし、h11~h32までをoutputとします。カスタムノード内のコードは下記になります。
float x00 = P1.x;
float y00 = P1.y;
float x01 = P4.x;
float y01 = P4.y;
float x10 = P2.x;
float y10 = P2.y;
float x11 = P3.x;
float y11 = P3.y;
float a = x10 – x11;
float b = x01 – x11;
float c = x00 – x01 – x10 + x11;
float d = y10 – y11;
float e = y01 – y11;
float f = y00 – y01 – y10 + y11;
h13 = x00;
h23 = y00;
h32 = (c * d – a * f) / (b * d – a * e);
h31 = (c * e – b * f) / (a * e – b * d);
h11 = x10 – x00 + h31 * x10;
h12 = x01 – x00 + h32 * x01;
h21 = y10 – y00 + h31 * y10;
h22 = y01 – y00 + h32 * y01;
return 1;
[CustomNode]CalcInverseMatrix(逆行列変換)
ここでは上述のh11~h32(h33は常に1)をinputとし、o11~o33をoutputとします。どちらも3×3の行列マトリクスです。
float i33 = 1;
float a = 1 / ((i11 * i22 * i33)+ (i12 * i23 * i31)+ (i13 * i21 * i32)- (i13 * i22 * i31)- (i12 * i21 * i33)- (i11 * i23 * i32));
o11 = ( i22 * i33 – i23 * i32) / a;
o12 = (-i12 * i33 + i13 * i32) / a;
o13 = ( i12 * i23 – i13 * i22) / a;
o21 = (-i21 * i33 + i23 * i31) / a;
o22 = ( i11 * i33 – i13 * i31) / a;
o23 = (-i11 * i23 + i13 * i21) / a;
o31 = ( i21 * i32 – i22 * i31) / a;
o32 = (-i11 * i32 + i12 * i31) / a;
o33 = ( i11 * i22 – i12 * i21) / a;
return 1;
[CustomNode]GetInverseHomographyPosition(ホモグラフィー変換先からの元位置取得)
上述のoutputを受けて各ピクセルの変換元のUV値を算出します。
float s = h6 * uv.x + h7 * uv.y + h8;
float x = (h0 * uv.x + h1 * uv.y + h2) / s;
float y = (h3 * uv.x + h4 * uv.y + h5) / s;
return float2(x, y);
[Output]Mask(変換先の領域マスク)
取得される変換用UVは変形後の矩形の外側も計算されます。これ自体は繰り返し表現などにも使えそうなので矩形領域と分けて出力しておきます。出力部分のノードは0~1の判別をifを使えば明快ではあるのですが、パフォーマンスを考えてあえて使いませんでした。
MF_Homographyのサンプル
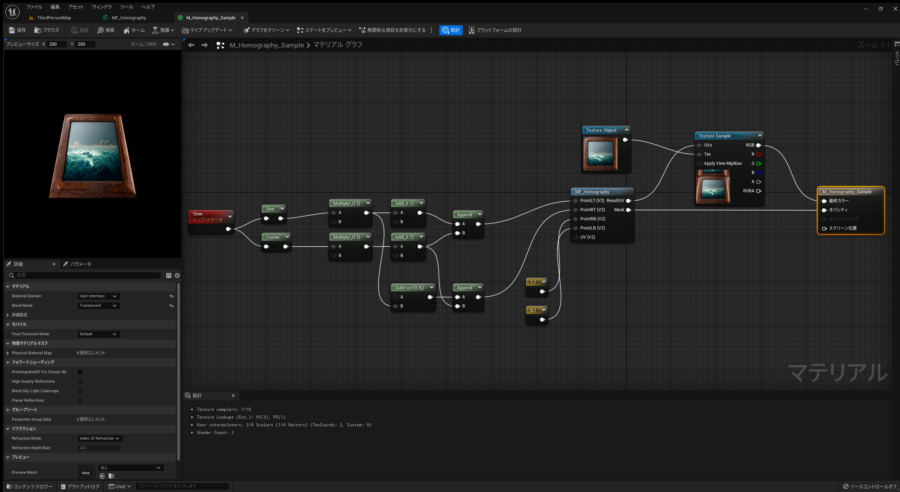
このマテリアル関数を使って作成したサンプルがこちらになります。
MF_Homographyを利用して台形変形を行うサンプル
MF_Homographyの入力はpointLT:左上, pointRT:右上, pointLB:左下, pointRB:右下の4点の変換先のポイントとUVを接続します。出力は変換されたUV(ResultUV)と4点による矩形の内側マスク用領域(Mask)となります。
今回は簡単にアニメさせるためにマテリアル内でTimeノードを使ってサクッと実現しましたが、4点のベクターをパラメータ化してグラフのシーケンサー上で扱えるのでより意図に合わせた取り扱いができると思います。
(ちなみにサンプル用のテクスチャはmidjourneyで短時間で作成しました、こういったことには非常に便利ですね。)
おわりに
とりあえずの移植とUEに合わせた実装は完了しましたが、下記の点で実用前に検証が必要だと考えています。が、それはまたいずれ、ということにしておきます。
- 関数のスリム化(逆関数などがそのままなので)
- マスク領域のアンチエイリアシング追加(エッジが立つので)
- Insightなどを利用してパフォーマンスを計測し、UMGのトランスフォーム機能との比較
実際のところ、このようなテクスチャの2D自由変形はUIグラフィック以外ではあまり使うことがないでしょう。狭い範囲での内容にはなりますが効果的なUI表現の足しになると良いと思います!